贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理,其中P(A|B)是在B发生的情况下A发生的可能性。贝叶斯定理也称贝叶斯推理.
P(A/B)=P(B/A)*P(A)/P(B)
条件概率
在事件B发生的基础上,A事假发生的概率,记为P(A|B)
从贝叶斯的公式来看有三个要素:
先验概率
P(A)为先验概率,即在不知道事件B的前提下,对事件A的一个主观判断
可能函数
P(B|A)/P(B)称为可能函数,这是一个调整因子,即新信息带来的调整,使得先验概率更接近真实概率
后验概率
P(A|B)称为后验概率,即在B事件发生之后,我们对A事件的重新评估
因此贝叶斯定理可以理解为:
后验概率(新信息出现后A的概率) = 先验概率(A概率) * 可能函数(新信息带来的调整)
贝叶斯的底层思想就是:
如果能够掌握一个事情的全部信息,就可以计算出一个客观概率.如果决策信息不全,只能根据有限信息,尽可能做出一个好的预测.在主观判断的基础上,先估计一个值(后验概率).然后根据观察新的信息不断修正(可能函数).
期望,方差,标准差,协方差
一个离散性随机变量的期望值是试验中每次可能的结果乘以其结果概率的总和
掷一枚公平的六面骰子,其每次“点数”的期望值是3.5
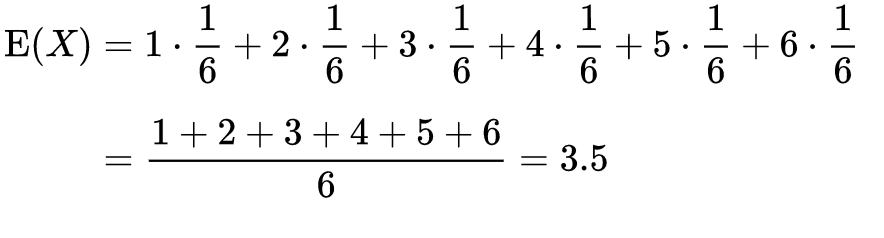
方差是用来衡量一组数据离散程度的统计量
标准差(standard deviation)等同于均方差(mean square error, MSE)。standard deviation英文译为“标准偏离”,事实上,标准差计算一组数据偏离均值的平均幅度,不管这组数据是样本数据还是总体数据
标准差是方差的平方根
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
从直观上来看,协方差表示的是两个变量总体误差的期望。
- 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;
- 如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
- 如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性,是一个衡量线性独立的无量纲的数。 协方差为0的两个随机变量称为是不相关的
联合概率分布
联合概率分布简称联合分布,是两个及以上随机变量组成的随机变量的概率分布。根据随机变量的不同,联合概率分布的表示形式也不同。对于离散型随机变量,联合概率分布可以以列表的形式表示,也可以以函数的形式表示;对于连续型随机变量,联合概率分布通过非负函数的积分表示。
联合概率分布分为联合离散型概率分布和联合连续型概率分布
离散型
对于二维离散随机向量,设X和Y都是离散型随机变量,{Xi}和 {Yj} 分别是X和Y的一切可能的几何,则X和Y的联合概率分布可以表示为如右图的列联表,也可以表示为如下的函数形式
连续型
对于二维连续随机向量,设X和Y为连续型随机变量,其联合概率分布,或连续型随机变量(X,Y)的概率分布F(x,y)通过一非负函数 f(x,y) > 0 的积分表示,称函数 f(x,y)为联合概率密度.
概率密度函数
连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
伯努利分布
伯努利分布亦称“零一分布”、“两点分布”。称随机变量X有伯努利分布, 参数为p(0<p<1),如果它分别以概率p和1-p取1和0为值。EX=p,DX=p(1-p)。伯努利试验成功的次数服从伯努利分布,参数p是试验成功的概率。伯努利分布是一个离散型机率分布,是N=1时二项分布的特殊情况.
二项式分布
二项式分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。二项分布的极限分布为正态分布.